SYSTEM BEHAVIOR: THE NEW RANGE
Bypass the Table of Contents and go the first page of the chapter.CHAPTER III - SYSTEM BEHAVIOR: THE NEW RANGE
- The Divergent Taxonomy - The Theory
- Definitions and Requirements
- Chaos
- Computer indeterminism.
- Nonlinearity.
- Nonequilibrium and energy.
- Sensitivity.
- Fractal.
- Universality. The laws of chaos.
- Unpredictability.
- Not chaos.
- Chaos
- The Taxonomy. Three Routes Into Chaos
- Comparison of Paradigm Theories
- Definitions and Requirements
- Chaos Research Across Many Disciplines
- Astronomy/Engineering/Chemistry
- Biology
- The Brain
- Sociology
- Social Systems
- Organizational Systems
- Research Difficulties in Chaotic Dynamics
- Comparisons of Research in the Paradigms
- Professional Practice and Chaotic Dynamics
- Comparing Paradigms for Professional Practice
- Synopsis of the Compelling Claim
CHAPTER THREE - SYSTEM BEHAVIOR: THE NEW RANGE
Prior chapters revealed an industrial age paradigm of education under strong criticism at all levels of the paradigm shell (figure 1-1), but a criticism whose intensity and perhaps effectiveness decreases in moving from the level of curriculum practice down to the bottom level of system behavior explanation. Even the curriculum reconceptualists applied their system explanation unevenly and their frequent centering of the cause of indeterminism in the high numbers of interacting variables has failed to achieve consensus (Phillips, 1987). As computer power explodes, complexity instills little uncertainty for many in the long confirmed axioms of the march of science towards greater prediction and control. Therein lies the special irony and power of the new potential source for reconceptualist confirmation and/or falsification of the old root axioms: hard science, scientists and their computing resources.As the proponents of a new view extend their taxonomy of interaction, effective confirmation and falsification science become the queen and king of the branch of system behavior with declining market share. Chaos theory's unfolding will proceed across the new taxonomy and up the paradigm levels as before. Because there is no prior educational research base for analysis as before, the critique of research must center on research across the other sciences, across the disciplines in steps moving ever closer to the door of education. But given the universality seen by chaos theory, this stepwise view would be seen not just as an advantage but essential, for like innovation theory and other system theories, chaos theory is insistently interdisciplinary. The comparisons that can now be made between the chaotic paradigm and the industrial age and reconceptualist paradigms will resolve which model is a more compelling model of interaction for education.
The Divergent Taxonomy - The Theory
Proponents of chaos theory claim that nature is dominated by nonlinear systems and that significant aspects of their long range behavior cannot be predicted in principle due to their sensitivity to the slightest perturbation. Yet there are a number of general laws and characteristics of these systems. This new division of system dynamics, perhaps due to its newness, goes by a variety of titles: strange attractors, deterministic chaos or chaotic systems. Weather is now seen as a prototypical example of a chaotic system, a system that diverges exponentially with time. The concept of the butterfly effect has emerged as one of its important metaphors. But as will be later seen, weather represents but one category of the divergent taxonomy. Further, such systems can have distinctive maps in state space. (See figure 3-1: Divergent attractor states; see also figure 2-7. Attractor table.)
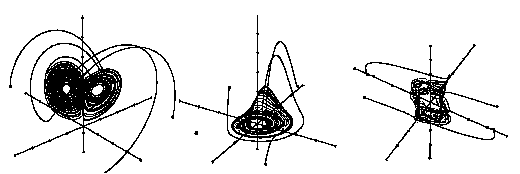 |
| Figure 3-1: Divergent Attractor States |
-
It is estimated that small perturbations are multiplied by four every week, or by 300 every month. This is what Lorenz calls the 'butterfly effect.' A butterfly's capricious flight may result in a tropical storm, not tomorrow, but one or two years down the road. ...No perturbation can be deemed too small to have any influence. (Ekelund, 1988, p.66)
The concept is so in contrast to the view of the industrial age paradigm that one is compelled to note that the quotation comes from a book that won a French award for technical accuracy in mathematical works for the layman, by an author of considerable reputation in his mathematical community.
The butterfly metaphor is the polar opposite of the principle stated by the 18th century French mathematician Pierre Simon de Laplace and noted by Dewey, "Were there a knowledge (in mechanical terms) of the state of the universe at any one time, its whole future could be predicted - or deduced"( 1929, p.202). "Although there are several obvious practical difficulties to achieving Laplace's goal, for more than 100 years there seemed to be no reason for his not being right, at least in principle" (Crutchfield et al., 1986, p.46).
The opposing concept of chaotic dynamics states that deterministic events in their interaction can and do produce uncertain and strange fluctuations for the human scale of observation. The butterfly effect assumes that next month's weather in China may be due to today's gentle flap of a butterfly's wings over a Wisconsin daisy (Gleick, 1987), but inherent divergence puts such a determination in principle, out of human reach. Chaotic systems diverge exponentially with time.
The phrase "deterministic chaos" would appear to be an oxymoron, a contradiction in terms, and yet understanding the strange juxtaposition is basic to understanding chaotic systems. Chaotic models may go in extremely different directions depending on minute differences in initial conditions, minute differences that researchers are unable to perceive or measure.
The concept of chaotic dynamics was discovered by many pioneers in many disciplines, but discounting the explorations of Poincare as tentative and largely ignored, the earliest in recent history is believed to be Edward Lorenz, in 1961. Lorenz had condensed a simulation of the weather down to 12 equations. The graphs and numbers in his printouts "seemed to behave in a recognizable earthly way. They matched his cherished intuition about the weather, his sense that it repeated itself, displaying familiar patterns over time, pressure rising and falling, the airstream swinging north and south" (Gleick, 1987, p.15). Needing to study one section of the graph at greater length, he used the data from that section as the initial data. In doing so he lopped off the figures from the 10,000th place on, since weather satellite's were lucky to read ocean-surface temperature to within one part in a thousand. The resulting new graph at first matched but then rapidly diverged from the original graph. Shortly, the weather patterns were so different they might as well have been initialized by different randomly selected values.
His work then gradually turned from weather prediction to modeling the essence of such strange behavior mathematically in as simple as possible deterministic equations (Lorenz, 1963a). Three innocuous looking equations capture the essence of the circulation of competing warm and cool air masses. They have been extensively analyzed (Sparrow, 1982):
-
dx/dt = 10 (y-x)
dy/dt = xz +28x-y
dz/dt = zy-(8/3)z
The independent variable T represents time, while X represents the intensity of the symmetric globe encircling westerly wind current, and also the poleward temperature gradient.... The variables Y and Z represent the cosine and sine phases of a chain of superposed large scale eddies, which transport heat poleward at a rate proportional to the square of their amplitude.... (Lorenz, 1984, p.102)
His 1963 article that introduced these concepts is heavily cited across the interdisciplinary chaos literature.
Von Neumann's 1950 dream of long range weather control has eventually faded from the meteorology agenda or at least has been redefined. A briefing prepared by leading weather researchers and sponsored by several national academies of science (Anthes et al., 1985) defined the "in principle" feasibility as around two weeks. The mathematician Ekelund commented:
-
Strangely enough, there was no problem with the mathematical model: the underlying physics was well understood, and the equations were safely written down. They were complicated, to be sure, even very complicated, but they were known, and they should have been helpful in predicting the weather with some degree of accuracy. Unfortunately, this was not the case.... (Ekeland, 1988, p.64)
As Lorenz himself noted, the theoretical hope for a reasonable 30 day forecast is now further away than it was 20 years ago (Lorenz, 1984), in spite of the tremendous progress in measurement, equation modeling and computer facility. The achieved measure of reliable long term forecast for global conditions is now about one week (Anthes et al., 1985).
A caution is in order in thinking about weather as a prototypical example. It has high value as a readily communicated and intuitively understood example. But there are other routes into chaos as will be seen later in this chapter. Without hard research data, it can not be determined which if any of these routes may be typical for educational phenomena. Rather, the immediate value of the weather example for this analysis is to make a point about determinism and offer an alternative basis for intuition to counter our educational culture's convergent heritage, in part derived from the mere chance that our nearby astronomical phenomena are so regular. "The beautiful regularity of Kepler's law, and the ensuing predictability of the solar system on the human scale, is an accident in celestial mechanics" (Ekeland, 1988, p.63). Think, says Ekeland, what form of inquiry might inform our culture had our celestial mechanics taken other possible forms.
Definitions and Requirements
The chaos literature uses a number of key terms with regularity. Other frequently used terms besides chaos are nonlinearity, non-equilibrium and sensitivity, fractal, universality and unpredictability. Later other closely related terms from the self-organizationist literature will be introduced in chapter four, but for now it is relevant to note that "in fact, chaos and self-organization turn out to be deeply related" (Davies, 1989, p.6). The psychological problem of using computers to generate indeterministic output also needs re-examination. Further, concepts such as chance, that look like related approaches to indeterminism, are not part of these concepts.
Chaos
The definitions for chaos are drawn from a wide variety of disciplines. In his summation of chaos literature developments prior to December 1983, Hao (1984) notes that "chaos is a rapidly expanding field of research to which mathematicians, physicists, hydrodynamicists, ecologists and many others have all made important contributions. ...It is a newly recognized and ubiquitous class of natural phenomena...." (p.i). He added that one must:
-
emphasize that chaos is not to be equated simply with disorder. It is more appropriate to consider chaos a kind of order without periodicity. Within generally chaotic regimes one can discover patterns of ordered motion interspersed with chaos at smaller scales, provided sufficiently high resolving power is reached in numerical or laboratory experiments. Instead of the usual spatial or temporal periodicity, there appears some kind of scale invariance.... (p.5)
Writings on chaos provide a variety of definitions for chaotic dynamics. This is not to say that the definitions are in conflict with each other, but rather a uniform definition does not appear to have merged. To Jensen, chaos represents "...(t)he irregular, unpredictable behavior of deterministic, nonlinear dynamical systems" ( Jensen, 1987, p.168). Crutchfield called it, "dynamics with positive, but finite, metric entropy. The translation from mathese (sic) is: behavior that produces information (amplifies small uncertainties), but is not utterly unpredictable" (Gleick,1987, p.306). To a physicist, chaos represented a kind of freedom, "(d)ynamics freed at last from the shackles of order and predictability ....Systems liberated to randomly explore their every dynamical possibility....Exciting variety, richness of choice, a cornucopia of opportunity" (Ford, 1986).
To John Hubbard, the randomness was nonexistent; ...simple processes in nature could produce magnificent edifices of complexity without randomness. In nonlinearity and feedback lay all the necessary tools for encoding and then unfolding structures as rich as the human brain. (Gleick, 1987, p.306)
The perhaps overly simple definition that summarizes all these definitions is that chaos is a system that diverges exponentially with time.
Computer indeterminism.
Some who have seen the printouts of variables or graphs of computer chaos simulations are struck by the precision with which the models repeat themselves. Having been led to expect the randomness of a random number generator (and any one run of data can look fairly random), they compare two runs of identical initial data and find them identical to nine or more decimal places at each iteration. Graphs laid on top of each other are identical. From this, they too quickly conclude that the concept of unpredictability is fraudulent. For if any one data point is known, any next point or series of points in time can be known, that is predicted for this run of the model and the next. The distinction lies between the precision of computer simulation and the fluctuation of real-world experiment. The reason computers became complexity-scopes (as in microscopes) is that they could easily do what humans would not, millions of iterations of simple nonlinear equations. This enabled the scientists to do what they have always done, test variations of their models. In so testing known fluctuations beyond their actual measurement capacity, new insights were revealed.
Nonlinearity.
Nonlinearity is an essential ingredient for chaos and is a term that must be considered by comparison with linearity. One of the major differences lies in a concept and set of interaction terms that has already been discussed: feedback, recursion and mutual causation. This concept of interaction was a concept reluctantly skirted by those reviewed when presenting aspects of the convergent taxonomy (e.g., Violato, 1988; Kenny, 1979; and Fisher & Ando, 1971).
Nonlinearity consists of equations containing terms which are repeatedly multiplied by themselves. Engineers would say they consist of two types: negative feedback loops such as the thermostats in our homes; and positive feedback loops such as the repeated sound amplification when a microphone is left too close to its speaker. The vocabulary for this interaction has perhaps been most fully developed by chemists. "The basic condition for the appearance of such phenomena is the existence of catalytic effects" (Prigogine, 1984, p.153). These feedback actions are "...comparatively rare in the inorganic world, (but) molecular biology has discovered that they are virtually the rule as far as living systems are concerned" (Prigogine, 1984, p.153). There are three basic patterns of catalysis: "autocatalysis (the presence of X accelerates its own synthesis), autoinhibition (the presence of X blocks a catalysis needed to synthesize it), and crosscatalysis (two products belonging to two different reaction chains activate each other's synthesis)" (Prigogine, 1984, p.153). It is but a small leap to imagine the effect of teachers' instruction and curriculum paralleling any or all of these forms of interaction. For example, individualized learning (the interactions within the brain system), and cooperative learning (interaction between minds), parallel respectively the ideas of autocatalysis and crosscatalysis. But in general, it would appear that most interactions in education are nonlinear.
Nonequilibrium and energy.
There is another basic condition that appears across the studies, high levels of energy or stimulus, whether internal (hormones and large energy supply) or external (stress, pressure), the energy necessary to drive a system to nonequilibrium. Schaffer notes that this single factor includes a variety of sources for stress, pressure or energy for the system (Schaffer, 1985). Energy levels can affect both the frequency of interaction and the depth of the interaction and thereby the rate at which a system diverges.
Sensitivity refers to the potential for the slightest change in a nonlinear equation to produce dramatic effects in the long term. The definition of long term lacks precision because it is relative to the time scale of the phenomena under investigation, from microseconds in the brain to a billion years in solar evolution. One of the tests of chaos has been to push its sensitivity to the edge of computer capacity. Seemingly insignificant variance in initial variables is critical. Wolf (1983) noted that variance of .000000000001 (12 decimal places) in a chaotic model created a difference of one part in 10 after only 50 iterations. Schaffer's computer could distinguish to fifteen decimal places and "the time series diverged after about 80 iterates" (Schaffer & Kot, 1986, p.59). While Briggs and Peat (1989) note that "even with the round off error minimized to one part in 31 places, determinism and predictability sputter... after only 100 iterations (p.73). ...Iteration pumps microscopic fluctuations up to macroscopic scale" (p.75). Remember that initial weather data, for example, is generally measured to the one-thousandth place (.001). Research estimates of the time for errors to double in weather systems has decreased steadily to current estimates that doubling occurs approximately every two days.
Would it be an overstatement to say that educational precision is less accurate than weather measurement? The more measurement precision is reduced, the more quickly the reliability of projections, extrapolations or predictions is lost, which amplifies any application of chaos theory to education. This suggests follow-up research to Cronbach's observation of a "half life" in educational data (1975). On what scale and to what degree does educational error double? Can we determine if the doubling rate is increasing or decreasing or stable? Could error doubling on the scale of the individual learner be a measure of creativity or inventiveness? Do we have sufficient time series data to run these calculations or must data be collected? Later, the problem of taking such measurements in education will be considered.
Fractal.
Mandelbrot (1983) insists that all chaotic attractors are fractal and deserve the better name of fractal attractor. Fractal is a term coined by Mandelbrot to refer to irregular fragments. These fragments represent a description of the grainy and irregular nature of many forms and systems through the use of rational and irrational numbers. This irregularity however is within scale. The irregularity becomes regularity by repeating itself across scale, such that at whatever magnitude of examination, the pattern persists, or becomes pattern within pattern. Such is the case with chaotic attractors. Numerous publications (e.g.: Mandelbrot, 1983; Peitgen & Richter, 1986) and computer programs now display and generate fractal images. Verbal description is inadequate to indicate their complexity and beauty, but it must be kept in mind that these published fractal images are two dimensional, though three dimensional work has been done in modeling all manner of phenomena, from imaginary planets to mountains and clouds. Further, the mathematical transformations to transfer a static fractal image to a three dimensional chaotic dynamic in motion have been demonstrated (Barnsley, 1986).
Universality. The laws of chaos.
The nature of prediction within chaos theory is twofold, for it exists, yet is denied on the practical scale for the long term. The predictability, the repeatability occurs across scale. "One of the great triumphs of modern dynamics has been the association of 'universal', i.e. system-independent, scaling laws with the changing parameter values" (Schaffer & Kot, 1986, p. 58). Feigenbaum discovered this one-dimensional map universality in 1976. "After many period-doublings, the intervals in lambda between successive doublings shrink geometrically by the same factor, a = 4.66920..., for all maps with quadratic maxima" (Wolf, 1983, p. 305). The universal number means that "when a system works on itself again and again, it will exhibit change at precisely these universal points along the scale" (Briggs & Peat, 1989, p.64). The equations explored for this universality vary from those for electrical circuits to business cycles to populations. Also, there is experimental confirmation of other universal characteristics: "the order of appearance of the various periodic states with increasing stress...was independent of the exact form of the map; ...the spacing between elements of period-doubled orbits; the effect of external noise on these states; and the character of intrinsic 'dynamical noise' (noise reflecting the aforementioned sensitivity to initial conditions)" (Wolf, 1983, p. 305).
Unpredictability.
The concept arguably the most confrontational to the industrial age paradigm is the concept of unpredictability. Raising the issue of indeterminism is not an idea new to chaotic dynamics. Heisenberg established the uncertainty principle early in this century. He established that there are aspects of knowing that are inherently intrusive and that can not be outmaneuvered. For example, one can accurately determine the position of the quantum particle or its speed but not both. Godel uncovered the incompleteness theorem (Hofstadter, 1979). No theory can be devised that will explain all theories or all possibilities. Every theory has its blind spot. Further, given our reliance on the real number system, all measurement is probabilistic (Ford, 1989). The relevance of chaotic dynamics is that it amplifies these claims, by showing the possible outcome of systems with inevitably uncertain beginnings. As a result, Mandelbrot has argued that a second stage of indeterminism has been introduced, a stage beyond the first stage indeterminism of past probability theory (Mandelbrot, 1987). "Exact prediction is both practically and theoretically impossible. Nonlinearity has dashed the reductionist dream" (Peat & Briggs, 1989, p.24). Even probability theory must face the understanding that trivial events can be sufficient to send the averages on a new course (e.g., the ice age fluctuations in long term climate).
Not chaos.
It is also important to discuss features that would appear to apply to chaotic systems, but do not, chance and variable complexity. What is now being explored as chaotic behavior has often in the past been ignored as white noise or randomness. The unpredictability of chaos models does not come from chance. "The concept of chaos excludes non-deterministic stochastic processes, such as the Poisson process or random walk" (Glass, Goldberger, Courtemanche, Schreir, 1987, p.10). Also, variable complexity, a high number of variables, is not a requirement. A simple equation generating chaotic dynamics may contain but three terms, i.e. May's (1974, 1976b) equation, X = R X (1-X).
The Taxonomy. Three Routes Into Chaos
There are three known routes into chaos: period-doubling, intermittency, and crises. The concepts of period-doubling and terms such as period-two, three, etc. are important in understanding these developments. A simple system operating periodically has two basins of attraction. One could think of it as having two central tendencies, a tendency to migrate to one or the other setting. Increasing pressure in a chaotic system can double and continue to double the number of basins of attraction. This can continue until the variety of options appear apparently at random, the chaotic-like setting. Yet at particular forcing levels beyond the first appearance of chaos, new order, for example period three, can continuously re-appear and then disappear. The emergence from chaos of period-three, or three basins of attraction, is a defining characteristics of the period doubling route to chaos.
The first type found was the "infinite period-doubling cascade" (Grebogi, Ott & Yorke, 1987, p.238) that was discovered by Feigenbaum. The character of the second, the intermittent route or:
-
...orbit is as follows: The orbit appears to be a period-three orbit for long stretches of time after which there is a short burst (the "intermittent burst" of chaotic-like behavior, followed by another long stretch of almost period-three behavior, followed by a chaotic burst, and so on. ...The average duration of the long stretches between the intermittent bursts becomes longer over time. ...This phenomenon (as well as period-doubling cascades and crises) is very general; in other systems it occurs for other periods (period one, for example) in easily observable form. (Grebogi et al., 1987, p.635)
The third, the crises route, will:
-
typically follow a chaotic-like path for a finite time, after which it finds its way out of the interval... and then rapidly begins to move to large negative values approaching negative infinity. ...Again, this type of phenomenon occurs widely in chaotic systems. For example, the model of Lorenz for the nonlinear evolution of the Rayleigh-Benard instability of a fluid subjected to gravity and heated from below has a chaotic onset of the crisis type and an accompanying chaotic transient. (Grebogi et al., 1987, p.635)
I now restate an earlier point that the Lorenz model for the weather is but one of the routes to chaos, and that educational researchers would need to examine their times series data from a variety of view points to confirm such behavior.
Grebogi et al. (1987) states that experimental support for these three routes into chaos is exhaustive. For instance, period-doubling cascades have been observed in the Rayleigh-Benard heat convection experiments, in nonlinear circuits, and in lasers; intermittency has been observed in the Rayleigh-Benard convection and in the Belousov-Zhabotinskii chemical reaction; and crises have been observed in nonlinear electronic circuits, in the Josephson junction and in lasers (Grebogi et al., 1987). "...Finally, all the routes to chaos are not known" (Grebogi et al., 1987, p.635). The divergent taxonomy, for now, then consists of three patterns: period doubling, intermittency and crises.
Comparison of Paradigm Theories
In looking back to the industrial age and reconceptualist paradigms view of system behavior, a number of comparisons of a theoretical nature can now be made with the view to weighing the compellingness of the chaotic paradigm. This analysis also considers the philosophical positions of Cronbach and Snow, Lincoln and Guba, Phillips and Krathwohl in relation to this new form of determinism, chaotic dynamics. It weighs the theory's direct refutation of scientific claims for identification of cause and its magnitude. It also considers the relative distribution of the convergent and divergent taxonomies of interaction. These thoughts in turn raise the issue of how we may have come to our convergent perspective in the development of statistics. Finally, three problems of psychological perspective will be considered: margins of error, paper media for communicating dynamic situations, and higher-order thinking skills.
By what means should compellingness be determined? Two simple criteria will be considered: 1. realism, or correspondence with reality; and 2., simplicity, Occam's razor.
Realistically, the evidence that such behavior occurs both in simulation on computers and in reality is, as Grebogi et al., (1987) states, exhaustive. There is also a sense in which chaos theory is simpler in its modeling of complexity because the industrial perspective requires a large number of variables for its complexity, while chaos theory does not. Further chaos theory is inclusive, not denying the convergent taxonomy, but noting its relationship to chaos. On both grounds, then, the theory of chaos, as a theory of divergence is more compelling. Other chaos concepts are also more realistic, but not necessarily simpler: nonlinearity, non-equilibrium, sensitivity, fractal and unpredictability. It is not that convergent perspective is necessarily wrong, but rather, it is inadequate to express the full range of dynamic behavior.
Phillips's claim (1987) that new theory will continue to simplify and therefore continue to cut through the fog of complexity to yield prediction and control is falsified by the reality of chaotic dynamics and by algorithmic complexity theory as well. Chaotic dynamics however gives a better account than complexity theory for systems that diverge with time and hence provides Cronbach a model to explain his generalization of half-life and decay in educational research. Yet the chaotic model supports Phillips's criticism of Lincoln and Guba's (1985) simultaneous interaction concurring that there is always some time lapse between events. But chaotic dynamics refutes Phillip's claim for long term prediction and control of cause and effect. That is, one can agree with this criticism of Lincoln and Guba and yet note the unreality of Phillips's position for salvaging falsification.
This problem with falsification and confirmation is true even for computers. "...A Cray 1 and a Cyber 205 gave wildly different answers by just the 50th point in the trajectory, due to the different roundoff mechanisms of the two machines" (Cipra, 1988, p.1162). The extreme sensitivity also furthers the case for holism, and such sensitivity is supported by ample empirical data, as will be further reviewed in the next section. Though, at the biological level, the data is more open to conflicting interpretations. Yet, chaos theory also challenges the absolute indeterminism of the reconceptualists, making specific allowance for normal scientific experiment in the short term. Future debate will most likely center on the definition of short and long term for a given phenomena.
But not only will the particulars of a diverging system be impossible to falsify, but it will be even harder to carry out Krathwohl's objective of confirmation. These issues would appear to require Krathwohl's consideration in a future chapter on cause and effect in social research and challenge his intuition about equilibrium being a natural attractor for an instructional setting. This is not to say that equilibrium could not be a natural state for some behavior, but that such behavior must allow for a much wider range.
This issue of equilibrium raises Porter's underlying observation (1986) that statistics rests on an assumption that events will average out. Clearly, such new nonlinear dynamics change at least the meaning of what it means to average out. An average could be computed, but that this number represents some settling out is clearly false and with it goes the "the ability to identify causes and estimate their magnitude" (Porter, 1986, p.318). The nonequilibrium of chaotic dynamics is not simpler than the averaging out of the equilibrium model, but it has already been shown to be realistic for a wide range of real world phenomena, and more examples will be forthcoming.
It is also of interest to speculate on the absence of nonlinearity in the conceptual tools first used to explore randomness, that is gaming and dice. Computers represent the first game tool capable of integrating nonlinearity. Like Ekelund (1988) speculating on the conceptual impact of different solar systems, where would our mathematical thought now be if someone could have engineered a gaming device a century or two ago where one roll affected the next? This thought represents at least some agreement with Streibel (1986) that there are some parameters to tools, which if they do not determine their use, at least reinforce certain perceptions. But the ideas presented here continue to reject the claim that tool (e.g., computers) use mitigates against creativity and innovation. In a curious form of reverse innovation, the nonlinearity explored on the computer has led to the building of a host of simple nonlinear mechanical devices that physically demonstrate the concept of chaos (See Abraham, 1985 and Gleick, 1987 for descriptions). But the point here is that nonlinearity more realistically describes the vast bulk of system behavior than does the linearity of the industrial age paradigm.
The frequency or distribution of chaotic dynamics compared with convergent systems of the industrial age paradigm is equally relevant to the weighing of the realism of chaos theory. "Chaotic phenomena are not just a motley collection from the mathematical labyrinth, but a wide class of natural events found in the physical world. Generally speaking, chaos happens more frequently than order, just as there are many more irrational numbers than the rationals" (Hao, 1984, p. 73). Others put the case even more strongly. "The important thing to note is that there is increasing evidence that for a given dynamical system, chaos seems to be the typical case, whereas in contrast to hitherto held beliefs, fixed points and oscillations are in a certain sense exceptions" (Haken, 1983, p. 24). Of these exceptions, the physicist Ford states, "Newtonian dynamics is now seen to be useful only for the nonrandom orbits of slowly moving, macroscopic objects, a collection of orbits whose relative size is perilously close to zero" (Ford, 1989, p. 354). From their new found perspective across many disciplines, the pioneers in this field began to reflect that a fair quantity of the research agenda was biased toward the exceptions, the fixed point and limit cycle assumptions, perhaps inevitable by-products of the industrial age paradigm. As if to correct this imbalance, some universities began setting up departments of nonlinear science, prompting "...noted pioneer in experimental mathematics, Stanislaw M. Ulam, to remark that this is like referring to the bulk of zoology as the study of non-elephants" (Campbell, 1985, p. 374). In brief, systems capable of deterministic chaos appear to be very common.
Chaotic systems are continuously iterative and recursive systems. The uncertainties (margins of error) are multiplied where variables are functions of each other. The outcomes of sufficient interaction are fluctuations, some of which can be highly amplified. Far-from-equilibrium, old structures can crack and new ones can form. Systems emerge that use the energy that drives the interactions to become self-reinforcing and persistent. In this manner, spiraling higher orders of life have come into existence. From a reductionist industrial age point of view, then, the living (including you and me) and other potentially chaotic driven systems, are multiplied margins of error. Though this concept is accurate and therefore realistic from the industrial age view, it is a particularly backward and more complex way to think about the self-organizing systems that defeat entropy and spiral into ever higher orders.
Of lesser but still genuine concern is the problem of the paper and text medium as a communication system across paradigms. The conceptual shift or the gestalt shift involved with a paradigm shift involves more than words. Words are generally an inadequate vehicle for developing understanding and intuition about systems in motion that evolve over time. Static two-dimensional models face similar difficulties. Adequate time to play with and explore such systems greatly facilitates understanding. The computer medium provides a readily available means for such activity. Commercially available programs for such exercise are already available through at least two sources: Aerial Press, which publishes related work developed by students and faculty at the University of California, Santa Cruz (see reference Aerial Press); a wide array of software tools from the University of Arizona, the product of Schaffer and others (Schaffer & Truty, 1988). The Aerial Press source also provides films and videos. For those with some programming background, the amount of coding is not strenuous. It is clear that the pioneers in this area all made the leap of intuition through extensive amounts of time exploring the interactions of graphic nonlinear models evolving with time. So, readers of chaotic dynamics concepts should consider whether any misunderstandings or difficulties come from problems with the writer's prose or with the inadequacy of written text itself and static pictures inherent to writing and where appropriate seek out further experiences. This then reinforces the idea that chaos is indeed borne of a new communication technology and to a degree generally inaccessible without computers. That is, nonlinear chaotic dynamics greatly benefits from a medium of communication beyond linear text, and the nonlinear multi-media capacity of computers appears a more realistic match.
The diverging nature of such systems also makes them realistic models for higher-order thinking skills and innovation theory. From this perception, many of these ideas of chaos theory do not represent new concepts to the educational literature. These educational terms in turn invert a common perception of chaos as negative. Consider the definitions of the innovation theorists. Innovation "represents any significant alteration in the status quo intended to benefit the people involved and represent something new to the people being changed (Havelock, 1973, p.4) or represents "...the adoption of means or ends that are new to the adopting unit" (Downs, 1976, p.3). Here an order, the status quo, is disordered through a new idea, a higher order, but viewed in a positive way. In turn, the concepts of creativity and invention parallel this perception. The paradox is the disorder created by new order, an essential tension that is also well documented by the innovation theorists (Rogers, 1983). Such a process appears inherently messy, but a messiness that builds a desirable complexity that by comparison makes the desire for simplicity more comparable to a form of a death wish where the health of living systems is concerned. This is a view in striking parallel to Igor Shofarevich's (1980), the noted Russian mathematician, in his analysis of the implicit nature of the long history of social efficiency cultures.
A problem remains for chaos theorists in their dependence of computers for their experimental mathematics. Given the roundoff error problem in computers noted earlier, what proof exists to show that the patterns observed are not just artifacts of the machine? The validation of their research tool will be evaluated in the next section's consideration of the research based on this theory.
Several thoughts summarize this section's overview of the theory of chaotic dynamics. Chaos can briefly be described as a system that diverges exponentially with time. Indeterminism results from the uncertain nature of the input for nonlinear equations; from the perspective of the industrial age paradigm, the margins of error are multiplied. Sufficient interaction in the catalytic sense is essential for chaos to form. There are many routes into chaos, with weather being but one example of a chaotic system, albeit a very useful one. The interaction discussed here resonates with Cronbach's and others' concerns with interaction in educational research. Also, the theory claims a greater realism, especially for phenomena for which linear modeling bogs down, the building of diverging complexity, and further, in certain circumstances, claims a greater simplicity as well. Finally, the nonequilibrium nature of the theory would appear to provide a more compelling model for higher order thinking skills than the equilibrium assumption of the industrial paradigm.
Chaos Research Across Many Disciplines
Dewey's argument with the humanists (1929) over the incorporation of scientific research into educational inquiry was based on a faith that educational inquiry could learn from being open-minded about continuing developments in science. His argument prevailed. As Sawada and Caley have commented, "The science of education has been largely a matter of adapting theories from psychology, sociology, biology, or other base disciplines and applying them to problems in education" (1985, p.13) This section on research affirms that same spirit. The focus now shifts from outlining the basic ideas of chaos theory to reviewing the depth and interdisciplinary range of research, gauging the power and the potential for an emerging consensus. A more systematic effort corroborates and extends the earlier evidence from physics and mathematics. Related work in astronomy, engineering and chemistry will be kept brief in order to put more emphasis on disciplines and fields closer to education. These ideas and discoveries are organized to build in stairstep fashion to the door of education.
Astronomy/ Engineering/ Chemistry
The rapid confirmation of chaotic dynamics seems further proof of Hanson's theory ladenness of observation. The diverse fields of astronomy, engineering and chemistry reveal substantial work in this area.
Increasing numbers of robust examples can be found in the archetype discipline of astronomy. The New York Academy of Sciences devoted a recent volume to the topic (Buchler & Eichhorn, 1987) discussing among other events, stellar pulsation, galactic models and solar sunspot cycles. From our own solar backyard comes confirming data in several phenomena. Wisdom (1987) in his Urey Prize lecture, notes confirming data in Saturn's tumbling satellite Hyperion and past behavior of other irregularly shaped objects, the distribution of asteroids forming the Kirkwood gap and the chaotic orbit of Pluto. If Pluto is chaotic, its "irregular motion will chaotically pump the motion of the other members of the solar system" (Sussman & Wisdom, 1988, p.437), producing chaotic behavior in the long term for the rest of our solar system.
Thompson and Stewart (1986) reviews chaotic dynamics from an engineer's perspective. While modeling a number of physical models for chaotic behavior, he uses the theory to emphasize the need for engineers to fully test the parameters of their models. More recently, computer science engineers Huberman and Hogg found that chaotic dynamics, including extreme sensitivity, were emerging in the use and allocation of resources in computer networks, a problem that has led to the development of another subfield, computational ecology (Angus, 1988).
The work of the Nobel laureate chemist Prigogine has extensively documented chaotic chemical systems, both organic and inorganic (1984). The classic inorganic case is the Belousov-Zhabotinskii reaction (Berge, Pomeau, Vidal, 1984) which produces spontaneous wave forms during the oxidation of citric acid by bromate in the presence of cerium ions (see also Peat & Briggs, 1989).
In general, the exponential growth in dissertations related to chaos theory, should be noted. By my count through the 1988 year of the Dissertation Abstracts Database, there are some 67 completed studies, the bulk of which are in engineering, physics and chemistry but also include economics, biology, ecology and computer science. However, no dissertation ( as of 1988) has been published that examines the relationship between education and chaotic dynamics.
Biology
Initial leadership in this area within biology is generally given to Robert May of Princeton University through his series of articles on chaos published in the 1970's (May, 1974, 1976a, 1976b, 1980). Analyzing the logistic difference equation,
N = RN (1-N), next N
he described the remarkable features of such an equation. In spite of its simplicity, it forms a bewildering number of solutions (1974). He pleaded for researchers to help others expand their intuition about natural systems as opposed to the intuition generally gained from studying physical systems by exposing others to the "wild things that simple nonlinear equations can do" (May, 1976b, p. 459). He surmised that there are:
-
countless situations outside population biology where the basic equation applies, such as genetics, epidemiology, economics (commodity, quantity and price, business cycles and other economic time series) and the social sciences (for example, theories of learning where X may be the number of bits of information that can be remembered after an interval t, or in the propagation of rumors in variously structured societies where X is the number of people to have heard the rumor after time t). (May, 1976b, p.459)
Others have confirmed his speculations. Chaotic models have been used to provide reasonable though challenged explanations of measles outbreaks (Schaffer and Kot, 1985b) and shifts in lynx populations (Schaffer & Kot, 1985a) and in ecological systems in general (Schaffer, 1985). Schaffer noted that the route to chaos was considered by and large a mathematical oddity ("mathematical curiosity" (May, 1976b, p. 155) that did not apply to biology, since populations did not reproduce (internal forcing) at a rate that matched the logistic equation parameters that produced chaos. Schaffer and Kot note that "since in many cases population numbers nonetheless fluctuate dramatically, we are further led to conclude that external forcing in the form of environmental variation is paramount" (1985a). In other words, the animal in question may not have a natural growth rate parameter sufficiently high enough to fit models of chaotic behavior. Yet when the system is in its natural setting, a variety of ecological system stresses have the effect of increasing this parameter. This enables the chaotic model to explain the overall long term unpredictable behavior so frequently observed in natural animal systems.
The Brain
Before considering the possibility that chaos theory models operations in the brain, it is worth a reminder as to the giga-neuron complexity of the system and its plasticity. "The human brain is probably the most complex sytem we know. ...According to present day estimates there are 10 to 10th power to 10 to the 11th power neurons in the brain. Plus, an individual neuron may have several hundred or more dendrites as input lines transmitting signals from other neurons." (Haken, 1983, p. 20) Recent studies also show significant neuronal growth within minutes of learning experiences. Neuronal linkage grows and dies in great sensitivity to the environment (Kotulak, 1988, p.2). How does our intution match reality here? Do we not suspect that behavior as complex as ours requires great governing complexity, since our behavior is so complex?
However, there is another explanation for such behavior:
Simple parameters such as the weight or the volume of the brain apparently mean very little (the blue whale being a notorious counter-example!). ...On many occasions we witness biological organisms with rather simple nervous systems (hardware)-like the leech or the cockroach - capable of very impressive and complex behavioral repertoires. So we come to expect that there are systems whose algorithm of information processing does not perhaps follow the principle of manmade artifacts of rising hardware complexity to achieve high complexity in the behavioral domain. (Nicolis, 1983, p. 330)
Nicolis shows that we can have a broad repertoire with very simple hardware since information in chaotically driven systems is not only produced by dissipating degrees of freedom but also by increasing resolution in systems with few degrees of freedom (Nicolis, 1983). Malburg notes that:
-
the contrast of this concept of organization to the cybernetical (psuedo-) concept of organization is extreme. In no sense are the organized states arbitrarily programmable, nor are they preformed in any palpable or coded form. The organized state is produced by the local interactions within the system, without there being the need for any global or centralized control. (1983, p. 240)
Simple parameters and low-dimensional systems are sufficient for the formation of highly complex behavior.
Avoiding high-dimensional problems (many degrees of freedom), researchers have tackled sub-components within the brain, concluding that:
-
...considerations suggest that we may expect chaotic processes in brain function at various levels starting, e.g., from neuronal activity up to the collective action of neuronal nets. ...The difficulty consists of adequate analysis, whether the case under study serves just as a random generator of signals or whether it carries a meaningful message (as words in a language). (Haken, 1983, p. 24)
This concern is theoretically answered by Nicolis. He proposes chaotic models for mental information storage and processing (1983, 1985, 1986a, 1986b).
Guilleman and others surveyed a number of studies of brain cells and noted seven different processes that support the concepts of chaos theory. An example of one of these processes cited is the 1 cAMP (cyclic adenosine monophosphate) parameter sensitivity that defies deterministic analysis by stimulating, dampening or inhibiting depending upon concentration and experimental circumstance. (Guilleman, Brazeau, Briskin & Mandel, 1983).
This view has been tested and validated by others. "...Since chaotic behavior has been observed in even very simple dynamical systems, proving the existence of chaos does not, in itself, validate a theory any more than proving the existence of a limit cycle does. This paper probes the model in greater detail..." (Carpenter, 1983, p. 311). This study "...provides concrete examples of neural networks which can exhibit chaotic behavior for certain parameters. This...discussion of chaos complements, rather than replaces, an analysis of structured patterns produced in biological systems" (Carpenter, 1983, p. 311).
Nicolis claims that an even stronger case can be for the incorporation of chaos theory:
-
To sum up: we have tried to appreciate why a cognitive system must be chaotic in order to perform effective signal processing. The answer can be offered a) in the time and b) in the frequency domains: a)by creating a MARKOVIAN time-division multiplexing the system allows separation of sensory modalities and it relegates for each one of these modalities a time-processing interval commensurate with the rate of sensory input. b)turbulent chaos (nonequilibrium noise) as a modus operandi of the thalamo-cortical pacemaker under mild excitation contains a broad spectrum of temporal (and spatial) frequencies, so it can constrain "patches" of post-synaptic functional areas in the cortex and create coherent patterns which can match a wide variety of incoming (spatial) temporal patterns. (Nicolis, 1983, p. 339)
Skarda and Freeman approached their brain study from a cognitive science frame of reference. In identifying brain patterns, they found:
-
...results that were beyond surprising; they took us so far outside the range of our previous expectations that we had no physiological metaphors with which to pin them down, and we had to draw on some new and fascinating fields of mathematics and physics in order to understand their implications (1987, p.162).
They found several instances in which chaotic dynamics is employed in the brain:
-
Special emphasis is placed in our model on "chaotic" brain activity. We propose that the brain relies on chaotic as opposed to steady or random activity for several purposes: Chaos constitutes the basic form of collective neural activity for all perceptual processes and functions as a controlled source of noise, a means to ensure continual access to previously learned sensory patterns, and as the means for learning new sensory patterns. (1987, p.161)
Rapp's work as a researching physician at the University of Pennsylvania's Medical College in collaboration with others also corroborates this effort. This work confirms a variety of chaotic signals in EEGs (Rapp et al., 1985). More recently this work has concentrated on mathematical and experimental technique for refining data acquisition and analysis, particularly working on the problem of the appropriate time scale for measurement ( Albano, Mees, deGuzman & Rapp, 1987 Albano, Muench, Schwartz, Mees & Rapp, 1988; Rapp, Zimmerman, Albano, Deguzman & Greenbaum, 1986).
To condense these notes on mental processes, the brain can be viewed as a rich environment capable of the full range of known system behaviors, including the chaotic regime. However, there is another theme that is emerging that must be considered before examining social systems. This further development of chaos theory is emerging in ecology, neurology and human physiology.
A revisionist school of thought wants to invert the view that the normal biological rhythm is a tendency toward equilibrium or a simple period as in the heart beat. It disagrees that a disorder will have a more complicated, less controlled nature. The revisionists have a number of examples that appear to falsify the older view.
Environmentalists have long argued that species diversity was a sign of biological system health, and the removal of species is a sign of an unhealthy environment. This concept is taken to a larger scale by the biologist, Lovelock (1988). He envisions chaos being used against itself to achieve global temperature stability. He sees in chaos an excellent mechanism for nature to prevent more violent longer macroscale fluctuations by shorter faster microscale adjustments due to chaotic fluctuations:
-
An ecologist friend of mine, C. S. Holling, has observed that the stability of large scale ecosystems depends on the existence of internal chaotic instabilities. These pockets of chaos in the larger, stable Gaian [planet Earth] system serve to probe the boundaries set by the physical constraints to life. By this means the opportunism of life is insured, and no new niche remains undiscovered. For example, I live in a rural region surrounded by farmers who keep sheep. It is impressive how adventurous young lambs, through their continuous probing of my boundary hedges, can find their way through onto the richer, ungrazed land on my side. The behavior of young men is not so different. (Lovelock, 1988, p.216)
To this variant behavior, I would also add the behavior in general of classrooms of children.
In a similar vein, Rapp noted in NOVA's 1989 television show reviewing chaos that the brain's use of chaotic dynamics is a superb exploitation that enables the brain to explore a full range of dynamic brain states with a minimal amount of effort. He appears to be supporting the view of the medical reconceptualists that "a healthy system has a certain amount of innate variability, and a loss of this variability - a transition to a less complicated, more ordered state - signals an impaired system" (Pool, 1989). Goldberger at the Harvard Medical School has analyzed normal and diseased hearts. Normal hearts may stay within a healthy range, but within that range their behavior is chaotic. Further, healthy hearts showed more variability in their beating than do sick ones. Goldberger's case is challenged by others who say that Goldberger's contention is far from proven.
There are other examples. Babloyantz and Destexhe (1986) compared epileptic and normal brain EEGs and though they found that both signals display chaotic dynamics, a normal brain is much more chaotic than when under an epileptic seizure. Skarda and Freeman (1987) see chaotic dynamics as a preparedness state that allows rapid response to completely novel as well as familiar input. Garfinkel suggests that "chaos in the body may be a way to avoid strictly periodic behavior, which could be very destructive" (Pool, 1989, p.606). Garfinkel demonstrates this simple process by holding a heavy book out from his body claiming that the eventual tremors represent loss of variability due to muscle fatigue.
Sociology
I have already noted that May was projecting in the 1970's that chaos theory would find application to human systems. His hunch was accurate. Two areas of sociology receive treatment here: social systems and organizational systems.
Social Systems
One of the first hints of chaotic dynamics in social systems came from explorations of data from economics in the 1960's. Mandelbrot, now a noted researcher in complex mathematics and fractals, described social phenomena that fits the chaotic system model. The data sets involved both the distribution of large and small incomes in an economy and cotton prices. He discovered that what appeared to be random fluctuation on one time scale corresponded to the fluctuation of values over long time periods:
Indeed, when Mandelbrot sifted the cotton-price data through IBM's computers, he found the astonishing results he was seeking. The numbers that produced aberrations from the point of view of normal distribution produced symmetry from the point of view of scaling. Each particular price change was random and unpredictable. But the sequence of changes was independent of scale: curves for daily price changes and monthly price changes matched perfectly. Incredibly, analyzed Mandelbrot's way, the degree of variation had remained constant over a tumultuous sixty-year period that saw two World Wars and a depression. (Gleick, 1987, p. 86)
Such self-similar patterns at different scales (fractal structures) are a common feature of chaotic system behavior (Mandelbrot, 1983; Gleick, 1987, Ford, 1989). Further, six dissertations have been completed on economic relationships to chaos through the 1988 year, most confirming the finding of chaos in the data.
Others have also noted the potential for a connection between sociology and the work done on chaotic dynamics and synergetics (Weidlich & Haag, 1983). These sociologists note that physico-chemical systems and societies share certain characteristics about their dynamic processes: they are both composed of many interacting units; each unit exists in one of several different states and makes transitions among these states. These systems differ in that the units and interactions of human society are "not of an elementary but of a highly complex nature" (Weidlich & Haag, 1983, p. 11). (This difference is lessened in that they make no reference to studies on chaos involving units of great complexity, e.g., general biological systems including ecology studies or neurological studies which include the human brain.) They also argue for another fundamental difference. "...In physico-chemical systems, the interactions lead to a "blind", i.e. unintended self-organization of the system, whereas the nature of interactions in sociology leads, at least partially, to intelligent "planned" structures" (Weidlich & Haag, 1983, p. 11). They do not however offer an opinion as to whether unintended self-organization or planned organization is better. (This difference is muted by the work of others studying management behavior that will be discussed later. They minimize the role of planned structures and prefer unintended self-organization.)
Weidlich and Haag's summarization of the dynamics and equations of motion in sociological systems is in general agreement with the foregoing discussion about equilibrium and non-equilibrium systems. They note, as have prior researchers, that "for a wide class of systems the random forces have no correlation with the macrovariables at the same or at previous points in time, rather they correlate with themselves over very short time periods ...In other words, infinitesimally small differences of certain "causes", i.e. the random forces, may lead to very large differences of the "effects", i.e. the paths of the macrovariables" (Weidlich & Haag, 1983, p. 5-6).
They also see that this in turn has a significant effect on one's ability to create prescriptions:
-
If the control parameters governing the dynamic behaviour of the system attain certain critical values due to internal or external interactions, the macrovariables may move into a critical domain out of which highly divergent alternative paths are possible. In this situation small unpredictable microfluctuations...may decide into which of the diverging paths the behaviour of the society will bifurcate. The branching into different possible scenarios at the bifuraction point may be accompanied or promoted by the rise in significance of new, hitherto unknown or irrelevant order parameters. ...The predictability with respect to the old set of macrovariables has been lost. (Weidlich & Haag, 1983, p. 13-14)
In other words, factors perceived as key at one stage of observation become irrelevant and replaced by others at a later stage of observation in an ongoing fashion.
There is a wide difference in the general predictive power of the traditional social, political and historical sciences and the natural sciences. Weidlich and Haag use the language of chaotic dynamics to explain this difference:
-
...The reason for this difference lies in the higher frequency of bifurcations and phase transitions in sociological systems as compared with physico-chemical systems. For instance, the unexpected rise or decline of macrovariables is a frequent process in sociology but a rare event in physics. As a result, in sociology the paths of macrovariables starting from neighbouring initial states may branch out into domains representing completely different situations. In terms of probability distributions an initially sharply peaked distribution will develop into a widely disposed multi-modal situation. ...Since processes in society are non-linear, bifurcations and phase transitions in this theory must be expected. These processes are accompanied by critical fluctuations making an unambiguous prediction of the future paths of macrovariables at critical points in time impossible, e.g., such a structure is incompatible with the assumption of a strict historical determinism. (Weidlich & Haag, 1983, p. 15-16)
These authors re-emphasize in their conclusion their belief that such modeling is descriptively useful in explaining behavior, but that direct modeling is impossible. "Reviewing the selection of scenarios presented in this section, one summarizing remark should be made immediately. The extreme sensitivity of the dynamics to the initial conditions and numerical values prohibits any use... for predictive purposes...." (Weidlich & Haag, 1983, p. 204). They further claim that this type of system behavior is common if not dominant in human social systems.
Organizational Systems
Moving from societies and cultures as a whole to social organizations changes the scale considerably. Yet this change of scale generally refers to a larger group than the handful of people referred to in small group research and obviously represents subsets of a culture. Institutions, firms, businesses or school districts, school buildings and classrooms are supersets of the arrangements studied in small group research. This discussion of organizational systems describes their examination and model building for interactive systems that parallels chaos research, but in a unique way. Organizational systems will be explored later in discussing how to overcome problems inherent in chaotic systems.
Organizational theorists have also seen chaos, though their approach to modeling is different and so is their terminology. Von Foerster notes the comparison to chaos theory, though he strongly prefers the term eigenvalues (self-values) instead of "strange attractor" when referring to the system's motivation. In another frame of reference, eigenvalue or self-value can also be described as will or will power. Eigenvalues apply at every scale, that is in every chaotic sub-system nested within other such systems. However, the example that he gives would today probably be considered a member of the previously discussed class of intractable problems raised by complexity theory.
Von Foerster in turn points theoretically to the work on finite systems by Gill (1962). Von Foerster's explanation of chaotic indeterminism is built on comparing two models, the Trivial and the Non-Trivial Finite State Machines, (TM and NTM). Both are conceptual devices with well-defined rules of operation. All the examples are his unless otherwise noted (Von Foerster, 1984, pp. 9-12).
The TM takes the following basic physical representation:
x --> (f) --> y
This structure can have many functions. In a "squaring" TM, x would stand for the integers 1,2,3,4 and y would become respectively 1,4,9,16. A supermarket TM senses code lines and the printer types "NOODLES ...$3.50". A deductive syllogism TM is produced by: "Socrates is a man" (the minor premise)"; All men are mortal" (the major premise); and the conclusion "Socrates is mortal." TMs appear under diverse names:
| X | F | Y |
|---|---|---|
| input | operation | output |
| independent variable | function | dependent variable |
| cause | Law of Nature | effect |
| minor premise | major premise | conclusion |
| stimulus | C.N.S. | response |
| motivation | character | deeds |
| goal | system | action |
For later comparison with a NTM, here is binary TM. Four input states f(x): A, U, S, T produce two output states (y): 0,1.
| f | ||
|---|---|---|
| X | : | Y |
| A | : | 0 |
| U | : | 1 |
| S | : | 1 |
| T | : | 0 |
The input sequence U,S,A will produce 1, 1, 0 forever.
TMs share the following characteristics: 1. predictable, 2. history dependent, 3. synthetically deterministic, and 4. analytically determinable.
An NTM differs in that a given stimulus may produce different responses. Externally, there appear no changes. Internally, things are quite different. Figure 3-2 is one version of an NTM.
The center circle is the internal state z. The internal state z and the input from x furnish an input to both the trivial machine F and the trivial machine Z. Z determines the subsequent internal state z'. Therefore, y = F(x,z), generally known as the driving function and z' = Z (x,z) is the state function. To facilitate clarity and comparison, only one more internal state will be added.
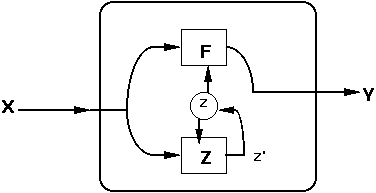 |
| Figure 3-2. NTM (a Nontrivial Machine) |
Testing the machine with several A's (A,A,A,...) would produce results similar to our previous TM, (0,0,0,....). The letter U produces consistent 1s. However, the S produces first a 0 and then a 1 and continues to flip back and forth. Testing the sequence USA produces either 111 or 000 depending on the initial internal system state:
| When in I | : | When in II | ||||
|---|---|---|---|---|---|---|
| x | y | z' | : | x | y | z' |
| A | 0 | I | : | A | 1 | I |
| U | 1 | I | : | U | 0 | II |
| S | 1 | II | : | S | 0 | I |
| T | 0 | II | : | T | 1 | II |
5 REM MAIN ROUTINE
10 LET Z = 1: REM CHOOSES INITIAL SYSTEM STATE
20 INPUT "PRESS ONE: A, U, S OR T.";X$
30 ON Z GOSUB 300,400
40 PRINT Y
50 Z = ZN
60 GOTO 20
70 END
300 REM STATE 1
310 IF X$ = "A" THEN Y = 0 AND ZN = 1
320 IF X$ = "U" THEN Y = 1 AND ZN = 1
330 IF X$ = "S" THEN Y = 1 AND ZN = 2
340 IF X$ = "T" THEN Y = 0 AND ZN = 2
350 RETURN
400 REM STATE 2
410 IF X$ = "A" THEN Y = 1 AND ZN = 1
420 IF X$ = "U" THEN Y = 0 AND ZN = 2
430 IF X$ = "S" THEN Y = 0 AND ZN = 1
440 IF X$ = "T" THEN Y = 1 AND ZN = 2
450 RETURN
From either the NTM flow graph or from the computer listing, one can generalize to the human condition. In different contexts, whether social settings or personal emotional situations, the same stimuli may produce different responses and then the nature of the response produce a following change in the context. As social beings and/or teachers, we seek to determine the internal states of others and respond appropriately.
If you are the computer user or the user of the NTM diagram, you do not see the inner features of the machine, but rather only see displayed the printed statements in line 20 ("Press one: U, S, A, T") and line 40, the current value of the Y variable. Seeing only the input and the output of the program or of the model, it would appear possible but cumbersome to reproduce the actual program. Each input and output would need to be laboriously recorded until the driving and state functions could be inferred. Von Foerster (1984) notes:
-
Alas, it is not so. Let me first turn to "cumbersome". The problem here is to identify among all possible machines with the given number of input and output states the one under investigation. ...The table...lists the numbers of the possible non-trivial machines with exactly two output states, say 0, 1... and with 2, 4, 8, 16 input states.
This machine has four input states A, U, S, T. An experimenter must search amongst 6.10 (76) different machines to find the right one.
Now to "possible". There exists a large class of machines whose driving and state functions are such that it is in principle impossible to infer these functions from the results of a finite number of tests: the general machine identification problem is unsolvable! This also means that there are non-trivial machines that are unknowable.
I shall summarize now the essential features of non-trivial machines.... In parallel to what I have said earlier about trivial machines, one can say that all NTM's are: 1. synthetically deterministic, 2. history dependent, 3. analytically indeterminable, 4. analytically unpredictable (p. 21-22).
Obedience is the hallmark of the trivial machine; it seems that disobedience is that of the non-trivial machine. However... the NTM too is obedient, but to a different voice. Perhaps, one could say obedient to its inner voice. (p. 10)
This inner voice has been called its eigenvalue or self-value or as I have suggested for the human context, will power.
Let us reconsider our model's input states and internal states in light of this examination of general system theory. From educational research, it is clear that there is a very high number of "x variables", inputs of varying importance in most educational settings. These alone, with the simplest of multiple internal states can create indeterminacy. But deterministic chaos shows that the internal states are not so simple. Replace the simplistic model of internal states provided by the NTM with our growing knowledge of system behavior. General system theory finds that to model reality, the function machine must have at least four internal states: the fixed point creates one kind of output, a stable equilibrium; the limit cycle output ranges from two to several; the torus produces a very high number of predictable outputs though within a very narrow space; and chaos outputs an infinite number of possibilities. Taken together in the NTM, the input variables and internal states produce a distribution that would appear to be infinite.
| The number of effective Internal States Z; the number of possible Driving Functions N(D) and the number of effective States Functions N(S) assuming One Two-Valued Output and One to Four Two-Valued Inputs. (only part of the table is presented here.) | |||
| n | Z | N(D) | N(S) |
|---|---|---|---|
| 2 | 4 | 256 | 65536 |
| 4 | 16 | 2.10(19p) | 6.10(76p) |
| Figure 3-3. Possible NonTrivial Machine States. | |||
While the previously discussed research has explicitly built upon or integrated the chaotic dynamics literature, there is an an area of investigation in educational psychology which is so suggestive of chaos models, that it deserves brief consideration here. The area is personality research and relationships to creativity. Farley (1986) has identified certain strong personality types noted for their aggressive and risk taking behavior. He further notes their correlation between these strong personalities, whether T+ (creative positive) or T- (creative negative), and increased hormone levels. That is in the language of chaos, an increase in the forcing variable, in this case the potent drug, hormones, produced divergent and discontinuous behavior, which was then applied in the culture in positive or negative ways. External stresses in the culture can combine with internal ones to raise behavioral outcomes to divergent levels.
To complete this walk through the research literature from physics to the social sciences toward our goal, Cronbach's Educational Researcher review (1988) takes us to the door of education, suggesting that educational researchers seek to apply the concepts of chaos theory to their work in the human sciences. In his review of Gleick's popular tradebook on chaos (1988), Cronbach notes some possible ways to apply chaos theory to the human sciences with examples of prior work resonant with chaotic dynamics, for example, suggesting that data collection while people are using computers or computer devices (e.g., sales check-out staff) may be one useful way to gather data for such analysis. He makes some general observations as well. The computer is essential in displaying incomprehensible numeric or algebraic data. Such research will require a great number of data points over time, a multivariate series, but "the human sciences have next-to-no experience here. Older time-series analyses... have rarely paid off for us" (p.49). Finally, there is some question as to whether the human sciences can meet the demands of techniques which are ravenous for large quantities of precise data.
Research Difficulties in Chaotic Dynamics
Educational researchers seeking to test chaos theory quantitatively face a number of serious and to some degree unsolved challenges. There are two general problem areas in doing such research: time series measurement and computer modeling validation.
As Cronbach previously noted, the quantitative study of chaotic dynamics requires time series analysis and this technique has posed difficulties in the past. It must overcome two hurdles for chaos research, extending test sensitivity and obtaining a large number of data points. With regards to sensitivity, a common technique is to ask the student one question each day to represent the understanding of a day's content in a subject area. The resulting data is either a 1 or a 0, an "on" or an "off." Providing more questions on a daily basis to increase test sensitivity is considered too time consuming to be practical. However, depending on a single question to represent daily success or failure is questionable. Secondly, the narrowness of the data range would appear to be insufficient for the graphic discrimination of chaotic attractors. Even if a picture did emerge, the noise in the system at this scale of data could obscure observation of a chaotic event. In addition to these difficulties, a high number of data points has been generally used in chaos research studies, from several thousand (Crutchfield et al., 1986) to several million (Skarda & Freeman, 1987). If a question could be asked of appropriate sensitivity every day of the year, the student would still only generate 365 plottable answers. The sampling rate then requires testing at least several times a day, a potentially highly disruptive process, though perhaps learners spending large amounts of time in computer environments could have measurements taken unobtrusively. Rapp and others (Albano, Mees, Guzman & Rapp, 1987) have given considerable attention to this problem. The lower bounds for resolution of chaotic attractors and determination of the correlation dimension appears to be around 500 data points, computing the appropriate variable to within "six percent of the literature value" (Albano, Mees, Guzman & Rapp, 1987, p.211), but this figure is subject to a host of qualifications. One of the qualifications is that the number of data points depends on the measure of dynamical behavior being considered, and there are several (Albano, Mees, Guzman & Rapp, 1987). Of these measures, "the correlation dimension has become the most widely used measure of chaotic behavior. It has been used in the analysis of hydrodynamic experiments, laser systems, neutron-star luminosities, neuronal and electroencephalographic signals, business cycles, etc." (Albano, Muench, Schwartz, Mees & Rapp, 1988, p.3017) but in spite of the fact that calculating the correlation dimension is an easy numerical procedure, "getting a dynamically meaningful number can be difficult, except in those instances where it is impossible"(Albano, Mees, Guzman & Rapp, 1987, p.218). For further consideration of the numerous issues see Albano, Muench, Schwartz, Mees & Rapp, 1988. This is not to suggest that failure is guaranteed, but that the process is daunting.
When such real world data are collected and examined, the results are compared with models of chaotic behavior that have been computer generated. The computer models represent the norm or meter stick against which actual data is judged. Given the round-off error in computers previously discussed, what assurance do we have that the resulting graphs are real trajectories and not machine artifacts? A proof has been proposed by Yorke and Grebogi (Cipra, 1988). The proof involves a simple test of the relationship from one point to the next on the trajectory, and this was done to the first 10 million steps of the Henon attractor. However, this confirmation does not go uncontested. Though "prevailing opinion among theorists is that the Henon map has a single attractor that is both chaotic and strange..." (Cipra, 1988, p.1163). Another possibility being explored is "...that the Henon map has infinitely many coexisting periodic attractors" (Cipra, 1988, p.1163).
In spite of the complications, the challenge of quantitatively refuting or confirming chaotic dynamics in educational phenomena appears within possible reach of educational researchers. Some combination of longitudinal and time series study can provide the necessary data, most likely in conjunction with the growing highly interactive educational computing environments. Prior work in a variety of disciplines has developed the techniques and computer tools for the required analysis.
Comparisons of Research in the Paradigms
In the prior theoretical section, the theoretical aspects of chaos theory were judged more compelling models of interaction for education than those of the industrial age and the reconceptualists. Following this review of research in chaotic dynamics, similar consideration for the research program of chaotic dynamics can now be undertaken. Educational researchers have in the past often borrowed from and modified the research programs of these other considered disciplines. Chaotic dynamics provides a new opportunity for such adoption, but basic questions must be weighed. Does the model of interaction in chaotic dynamics provide a potentially more compelling research program for education than does the industrial age paradigm, or the reconceptualist paradigm? This requires a review of the evidence for chaotic interactions, of the realism and simplicity of this evidence and comparison to older research programs.
The presented research evidence for chaotic interaction shows a high number of confirming studies as well as a high number of reporting disciplines, which bodes well for its claimed interdisciplinary nature. Further, the "harder" the science, the less controversy about the fact of chaotic dynamics, and yet the "softer" the science, the more nonlinearity dominates the nature of interactions in the discipline. It is reasonable then to see nonlinear interaction as a defining characteristic of both individualized and collaborative learning and higher-order thinking. This evidence implies that chaotic dynamics is a highly realistic model of interaction and most appropriate for educational adoption. However, the simplicity argument depends somewhat on whether the view is of the model or of the model's perceived outcome. The models of interaction for chaotic dynamics are simple ones, though it is clearly more complex than Krathwohl's first unidirectional model where A causes B but only slightly more complex than his multi-causal and feedback models. In terms of model outcomes, the convergent equilibrium view of the industrial age is clearly simpler than the nonequilibrium complexity into which chaotic models spiral. However, chaotic models of interaction have adequate simplicity for research purposes and allied with their realistic nonlinear nature, provide a model superior to the convergent or indeterministic models.
Further research comparisons with the industrial age paradigm support the more compelling view of the chaotic paradigm. The scientific method requires both a discovery and a test phase (Krathwohl, 1985), with post-positivists (Phillips, 1987) arguing that only falsification, not confirmation, is legitimate. Violato's analysis indicates that the very requirement for testability and repeatability can bias the researcher toward a rejection of the real situation. Violato rejects the use of several nonlinear models of personality because they "lose track of what specifically is caused... and what is constant through time" (1988, p. 9) yet also notes that "the bulk of data to date indicate that individuals do not demonstrate ...consistency" (p. 17), that is, constancy through time in personality. In other words, the nonlinear models he rejects describe the results that he reports but these are results that he does not accept because they violate the scientific method requirement for consistency, that is testable repeatability. The goal of the scientific method is to converge on laws and rules which allow the accumulation and higher organization of knowledge. But even in spite of the linear models often preferred by educational researchers, Cronbach's analysis stands unrefuted. Educational generalizations appear to decay with time.
Comparison with the reconceptualist paradigm reveals a different situation. Reconceptualists agree with the chaotic paradigm on the general long term outcome of research. It is uncertain, indeterministic. The differences are over the short term. Guba and Lincoln argue for no separation of cause and effect while the chaotic paradigm claims that for some indeterminant short term period, it is sometimes possible to follow Krathwohl's chain of cause and effect and apply the scientific method. The reality of the evidence considered so far in chaotic dynamics indicates that even for chaotic non-equilibrium environments, researchers have continued to find a time lapse between cause and effect allowing observation and measurement, which as Phillips argued (1987) undoes this reconceptualist argument, but only for the purposes of short term analysis.
Professional Practice and Chaotic Dynamics
Having considered the theory of chaos and research on chaotic dynamics, we turn to published discussion of relationships between chaos theory and professional practice. Published acknowledgement of the application of chaos theory and research to professional practice is nil. However, the three citations found were notable in their relevance to educational application: organizational management, educational policy and the elementary classroom.
Recent work in business theory indicates that both implicitly and explicitly, those thinking about business systems are recognizing the importance of themes parallel to those generated by the study of chaotic dynamics. The authors of the widely read book, In Search of Excellence (1982), have expanded on their earlier themes to produce new best sellers. Peters work, Thriving on Chaos (1987) contains a number of parallels which recognize the need to act on environments as chaotic systems, though in these books he does not reference or even imply that he is aware of the published work on chaotic dynamics. But his intuition has dealt with organization as if he had. However, after publishing The Renewal Factor(1987a), Waterman came across the chaos literature and concluded that these concepts relate specifically to the assumptions that he was making for organizational management. "If we want innovation and creativity in the U.S., which is what strategy was supposed to have been about in the first place, we need strategic processes that are robust and adaptive - ones that comprehend unpredictability and chaos" (Waterman, 1987b, p. 182).
The first publication to consider the relationship between chaos theory and educational practice, dealt with some general implications for educational policy (Houghton, 1988). After a long review of some of the highlights of the chaos literature, Houghton briefly and perhaps too subtly suggests a general direction for educational policy, increase the rate and depth of interaction among all members of the educational system. This has two corollary implications, implications for educational stability and cultural values.
Stability in chaotic environments comes not from preventing change and eliminating chaos as will be discussed in the next chapter. In nonequilibrium environments, chaos on one scale yields stability on a higher scale. That is microlevel chaos yields macrolevel stability through constant adaption to changing circumstances. Computer systems will be increasingly important channels for information flow in this mutation process. Chaos represents a healthy natural order of things, a special kind of fertility for innovation and intellectual growth.
Finally, the sensitivity of chaotic environments, where high levels of interaction pump microlevel events to macroscale outcome, makes the teaching of values and ethical principles important to social health. Chaotic dynamics indicate that there is no guarantee of beneficial self-organization emerging from chaotic mixing. In a system potentially sensitive in the long term to the slightest gesture, the eventual linkage among people of like value for periods of time will create groups of strength and power with the potential for strong positive or negative benefit.
Doll's work (1989) moves beyond general policy to the classroom. He provides an early attempt at abstracting from chaos theory for classroom application. He also notes the strong connection between the self-organization literature of the chemist Prigogine (1980; with Stenger, 1984) and the chaos literature. His work seeks to guide both curriculum and instruction.
In his work with elementary students every Friday in mathematics problem solving, he and the cooperating teacher made a number of changes. In curriculum, routine drills are eliminated. Problems are hard and challenging. Understanding is emphasized over memorization and creative utilization of patterns is emphasized over working set algorithms. As for instruction, they grant students "flexibility in their intellectual and social organization - they solved problems in their own way and in their own time" (Doll, 1989). But it became important to balance this flexible time with directed time in some indeterminant proportion. Teaching analysis (evaluation) of time spent should be in terms of shifts from chaos to re-organization, analysis "not in terms of time spent but in terms of the insights developed by the students" (Doll, 1989). They required collaborative work in teams of two and four in order to increase communication and thereby cooperation and re-organization. They innovated in curriculum content by introducing concepts from complexity fractal research but rejected computer use to explore chaos patterns in favor of simpler activities students could do with pencil and paper.
In retrospect of Doll's field study and Houghton's essay, one finds no curriculum and instruction ideas that have not surfaced in education before. The curriculum and instruction concepts employed bear close resemblance to the literature on teaching higher-order thinking skills (e.g., Patterson & Smith, 1985), to the general literature on gifted and talented education and resonates as well with Dewey and progressive education in the early part of this century. The call for ethics instruction becoming an integral part of education reaches even further back into the educational practices of the last century. The novel aspect appears to be the discovery of a deep theory that provides a rationale for marginalized patterns of education (e.g., Dewey's prgressive education, Piaget's learning dynamics, ethics education, developmentalists, social meliorists) that have long been advocated but have never dominated the educational scene in this century, yielding to the stronger efficiency theory of the industrial age paradigm. This efficiency theory could be stated as the belief that proper paths to learning can be determined, optimized and produced as a set of objectives and related materials and then be administered by teachers.
Comparing Paradigms for Professional Practice
Chapters one and two have already discussed the forms and many criticisms of the practice of industrial age education. From the industrial perspective it is reasonably simple to conceptualize and state certain initial parameters and form some expectation for what a curriculum and instruction system will do. That the study of the diffusion of innovation shows that divergence is common suggests that deeper analysis of the nature of highly interactive systems is required. Chaos theory provides that deeper analysis. Realism and simplicity provide the grounds for comparison.
There remains strong interest in maintaining the status quo interest in efficiency and in resisting fundamental change. "Never before has there been such widespread agreement that schools need to be reformed, restructured, and redesigned. There also seems to be fairly widespread agreement that schools will need to make better use of technology to meet future demands and to optimize efficiency" (Salisbury, 1989, p.2). Merrill recognizes that there are "serious limitations" with first generation instructional design theory because it has "little or nothing to say about highly interactive instruction and hence provides very little guidance for our current high tech media delivery systems..." (Shore, 1989, p.1). Yet he concludes that second generation theory should be formed. "The term 'second generation' is intended to imply that we don't need another alternative theory; rather, we should build on the fine work of the past...." (Shore, 1989, p.1). Unstated is just what highly interactive means, nonlinear, internal interaction or something else.
The compellingness of chaos theory for a model of interaction in educational practice must be tested against its realism and its simplicity. Chaos research provides a realistic model for what happens in highly interactive systems. They diverge in the long term beyond our predictive sight and beyond our control. The only way chaos models show that prediction and control can be maintained in nonlinear systems is through low levels of interaction, that is damping the system. The simplicity of chaos in its dependence on the system (learner) to self-organize defeats optimization but reduces the increasingly complex instructional design requirements. By comparison, Merrill's second generation instructional design incorporates three massive computer systems with many subsystems: a knowledge analysis and acquisition system; a transaction configuration system and library and a strategy analysis system. Either Merrill's systems must not be highly interactive, which contradicts his stated goal, or the interaction itself will defeat the hierarchical guidance he envisions. Before years of research go into building intricate and complex instructional designs only to have them fail in the classroom, the designers such as Merrill and Reigeluth (1989) must pause and develop a compelling model of interaction that counters the relatively simple current view of interaction (i.e., cause and effect, determinism) from chaos theory. If they cannot develop such a model for the highly interactive multi-media systems that are heir-apparent to today's educational computers, they must change a fundamental direction of their work. Schon, Peters, Houghton and Doll all suggest a number of ideas derived from an understanding of chaotic dynamics for those who wish to pursue an alternative to the dominant view of instructional design and later chapters will pursue this as well.
Synopsis of the Compelling Claim
The first hypothesis states: the model of interaction developed in the study of chaotic dynamics is a more compelling model for education than the model of interaction generally assumed by the dominant and prior reconceptualist paradigms. The examination of this hypothesis involved several stages. The second chapter provided a critique of the industrial and reconceptualist paradigms. This chapter reviewed the chaos literature from the levels of theory to research and practice. It made paradigm comparisons at each of these levels. Kuhn's criteria for a successful paradigm shift has been applied, requiring that not only chaotic dynamics appear a compelling alternative, but that significant aspects of the dominant industrial age paradigm be shown to be inadequate. Two other arguments also emerge, one circumstantial and the other historical. A further contribution is the development of the paradigm shells and a taxonomy of the range of system behavior.
The first means for refuting this hypothesis would be to show that the levels of the industrial age paradigm were robust and unassailable, that there was no need for change. The review of the literature at each level of the paradigm shell indicated otherwise. At the theoretical or explanatory level, the concepts of determinism and convergency continued to yield ground. The positivist test of confirmation gave way to the post-positivist test of falsification. But such falsification also requires repeatability over the long term of a system's behavior. Algorithmic complexity theory and chaos theory show that such determinism is impossible for broad classes of behavior, though chaos theory supports short term determinism in some divergent categories. The explanatory level of the industrial age paradigm and its supporting scientific method have suffered serious failures, changing the inquiry agenda from prediction and control to the identification and description of patterns of behavior.
The theory of the reconceptualists, both critical and naturalist, received a different reaction. Their theory was shown to indicate some tension or contradiction between their sense of determinism and indeterminism, but an overall weighing in on the side of indeterminism. Chaos theory presents a rigorous model that explains and accepts this tension. Chaos theory complements such theory more than it refutes it. A greater sense of the complement awaits the next chapter. The end result is that prior reconceptualist positions are augmented in some as yet not fully articulated way.
At the research level, to refute chaos theory's model of interaction for education, the gradual accumulation of the laws and rules of education needs presentation. Instead the literature finds that Cronbach's claim for educational generalization "half-life" stands unrefuted. As much reconceptualist work is based on the absence of prediction and control, chaos theory is generally complementary. However, chaos theory does make two alterations to the reconceptualist position. One change is the acceptance of experimental work over some indeterminant short term period. This would appear easier for the critical theorists to accept than the naturalists. The second change is the acceptance that amidst building turbulence, higher order can emerge in the long term and be positive as well as negative phenomena. Further, such phenomena provide patterns of development that can be studied and described and possibly predicted for short durations.
At the level of practice, the industrial age literature should show that factory model schools using efficiency as their guiding light are not only superior schools, but making steady improvements. To the contrary, the call for significant educational reform is unabated. Though this call for reform includes many voices speaking for ever greater efficiency, an idea that was shown to be based on a convergent perception of development.
In addition to the succeeding case against falsification of the industrial paradigm and the failing case against falsification of chaos, there are confirming arguments for its acceptance. A circumstantial argument is possible based on the similarities between the chaotic model and educational phenomena. One special area of similarity is nonlinearity (feedback and recursion). Another feature is the observance of chaotic dynamics across biological phenomena in general and brain behavior in particular.
The historical argument simply notes that there is a long history of experimentation and adoption of ideas pioneered in other disciplines. "The science of education has been largely a matter of adapting theories from psychology, sociology, biology, or other base disciplines and applying them to problems in education" (Sawada and Caley, 1985, p.13). Further, the evidence for its application to social science and education is comparable with the quality of the evidence Dewey presented for the application of experimental science (1929). That is, he did not offer evidence that the scientific method had proven itself effective in education in certain studies, but rather argued that the compelling nature of what was going on in the sciences required that it be given its due in education, and that a case against certain prior philosophical traditions was possible. Further, we see that concept of chaos is being actively borrowed across the other disciplines. That such ideas are compelling for science in general makes them compelling for education as well.
Two other contributions have been made for the purposes of this analysis, that stand outside it and yet give structure and form to the discussion. One is the graphic outline of the considered paradigms. An additional contribution of this work is the development of a taxonomy of system interaction that so far is divided into categories of convergent and divergent behavior, a taxonomy which has provided a means for communication across and about diverse paradigms, a communication which Lincoln (1989) and Guba (with Lincoln, 1985) have argued is not possible in principle or in fact.
The primary case that can still be made against chaos theory for education is that even though much has been explained, a major concern has been given insufficient treatment. If interacting nonlinear systems could describe education and these systems always go chaotic or diverge, how does any organization occur, any stability remain? Our classrooms and curriculum are not generally perceived as endlessly chaotic. How does one move from the nonlinear divergent side of the taxonomy to the linear convergent side? The control that has been hinted at (the E variable of the logistic equation explained earlier) is lowering the rate and depth of interaction, acts which in themselves sound generally educationally unpalatable, but which shut off chaotic dynamics and return us to the convergent side of the taxonomy. This conservation role, to retard innovation and creativity and thereby change, appears in this light to be one of the primary functions of hierarchies and this role is not without its beneficial function. After all, is more chaos what is really needed? On the other hand, can order be achieved with and through chaos instead of cancelling it to achieve order? That is, must the linear order and stability of our designs always be achieved through the sacrifice of nonlinear innovation, creativity and inventiveness?
Accepting the compellingness of the divergent taxonomy of interaction, how can one cope with such an environment? What aspects of educational theory and practice can provide concepts and activities to form a new model for educational inquiry? Chapters four considers the second hypothesis of the study and new grounds for integration and organization.
| Top of Chapter Three. | Chapter Four. | A Chaotic Paradigm: Table of Contents |
| Page author: Houghton | ||